Coordinate Systems
Getting-started/Coordinate-Systems
In the last chapter we learned how we can use matrices to our advantage by transforming all vertices with transformation matrices. OpenGL expects all the vertices, that we want to become visible, to be in normalized device coordinates after each vertex shader run. That is, the x, y and z coordinates of each vertex should be between -1.0 and 1.0; coordinates outside this range will not be visible. What we usually do, is specify the coordinates in a range (or space) we determine ourselves and in the vertex shader transform these coordinates to normalized device coordinates (NDC). These NDC are then given to the rasterizer to transform them to 2D coordinates/pixels on your screen.
Transforming coordinates to NDC is usually accomplished in a step-by-step fashion where we transform an object's vertices to several coordinate systems before finally transforming them to NDC. The advantage of transforming them to several intermediate coordinate systems is that some operations/calculations are easier in certain coordinate systems as will soon become apparent. There are a total of 5 different coordinate systems that are of importance to us:
- Local space (or Object space)
- World space
- View space (or Eye space)
- Clip space
- Screen space
Those are all a different state at which our vertices will be transformed in before finally ending up as fragments.
You're probably quite confused by now by what a space or coordinate system actually is so we'll explain them in a more high-level fashion first by showing the total picture and what each specific space represents.
The global picture
To transform the coordinates from one space to the next coordinate space we'll use several transformation matrices of which the most important are the
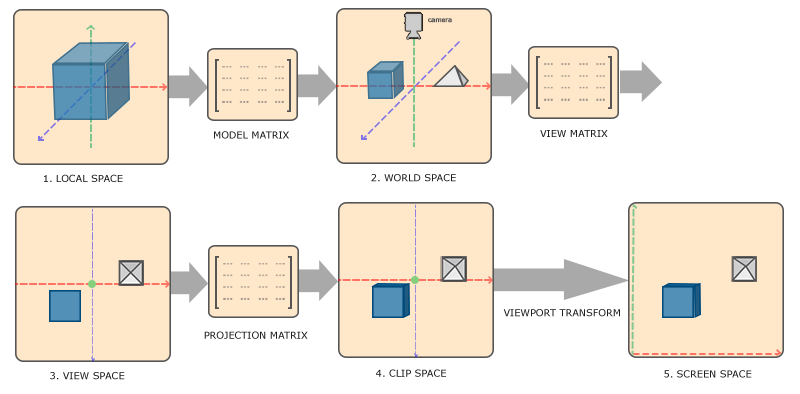
- Local coordinates are the coordinates of your object relative to its local origin; they're the coordinates your object begins in.
- The next step is to transform the local coordinates to world-space coordinates which are coordinates in respect of a larger world. These coordinates are relative to some global origin of the world, together with many other objects also placed relative to this world's origin.
- Next we transform the world coordinates to view-space coordinates in such a way that each coordinate is as seen from the camera or viewer's point of view.
- After the coordinates are in view space we want to project them to clip coordinates. Clip coordinates are processed to the
-1.0and1.0range and determine which vertices will end up on the screen. Projection to clip-space coordinates can add perspective if using perspective projection. -
And lastly we transform the clip coordinates to screen coordinates in a process we call
viewport transform that transforms the coordinates from-1.0and1.0to the coordinate range defined byglViewport
You probably got a slight idea what each individual space is used for. The reason we're transforming our vertices into all these different spaces is that some operations make more sense or are easier to use in certain coordinate systems. For example, when modifying your object it makes most sense to do this in local space, while calculating certain operations on the object with respect to the position of other objects makes most sense in world coordinates and so on. If we want, we could define one transformation matrix that goes from local space to clip space all in one go, but that leaves us with less flexibility.
We'll discuss each coordinate system in more detail below.
Local space
Local space is the coordinate space that is local to your object, i.e. where your object begins in. Imagine that you've created your cube in a modeling software package (like Blender). The origin of your cube is probably at (0,0,0) even though your cube may end up at a different location in your final application. Probably all the models you've created all have (0,0,0) as their initial position. All the vertices of your model are therefore in local space: they are all local to your object.
The vertices of the container we've been using were specified as coordinates between -0.5 and 0.5 with 0.0 as its origin. These are local coordinates.
World space
If we would import all our objects directly in the application they would probably all be somewhere positioned inside each other at the world's origin of (0,0,0) which is not what we want. We want to define a position for each object to position them inside a larger world. The coordinates in world space are exactly what they sound like: the coordinates of all your vertices relative to a (game) world. This is the coordinate space where you want your objects transformed to in such a way that they're all scattered around the place (preferably in a realistic fashion). The coordinates of your object are transformed from local to world space; this is accomplished with the
The model matrix is a transformation matrix that translates, scales and/or rotates your object to place it in the world at a location/orientation they belong to. Think of it as transforming a house by scaling it down (it was a bit too large in local space), translating it to a suburbia town and rotating it a bit to the left on the y-axis so that it neatly fits with the neighboring houses. You could think of the matrix in the previous chapter to position the container all over the scene as a sort of model matrix as well; we transformed the local coordinates of the container to some different place in the scene/world.
View space
The view space is what people usually refer to as the
Clip space
At the end of each vertex shader run, OpenGL expects the coordinates to be within a specific range and any coordinate that falls outside this range is
Because specifying all the visible coordinates to be within the range -1.0 and 1.0 isn't really intuitive, we specify our own coordinate set to work in and convert those back to NDC as OpenGL expects them.
To transform vertex coordinates from view to clip-space we define a so called -1000 and 1000 in each dimension. The projection matrix then converts coordinates within this specified range to normalized device coordinates (-1.0, 1.0) (not directly, a step called Perspective Division sits in between). All coordinates outside this range will not be mapped between -1.0 and 1.0 and therefore be clipped. With this range we specified in the projection matrix, a coordinate of (1250, 500, 750) would not be visible, since the x coordinate is out of range and thus gets converted to a coordinate higher than 1.0 in NDC and is therefore clipped.
This viewing box a projection matrix creates is called a
Once all the vertices are transformed to clip space a final operation called x, y and z components of the position vectors by the vector's homogeneous w component; perspective division is what transforms the 4D clip space coordinates to 3D normalized device coordinates. This step is performed automatically at the end of the vertex shader step.
It is after this stage where the resulting coordinates are mapped to screen coordinates (using the settings of
The projection matrix to transform view coordinates to clip coordinates usually takes two different forms, where each form defines its own unique frustum. We can either create an
Orthographic projection
An orthographic projection matrix defines a cube-like frustum box that defines the clipping space where each vertex outside this box is clipped. When creating an orthographic projection matrix we specify the width, height and length of the visible frustum. All the coordinates inside this frustum will end up within the NDC range after transformed by its matrix and thus won't be clipped. The frustum looks a bit like a container:
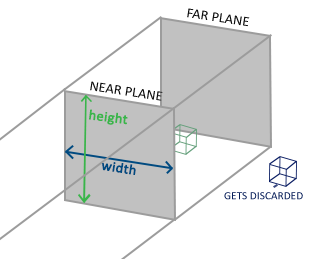
The frustum defines the visible coordinates and is specified by a width, a height and a w component of the transformed vector; if the w component remains equal to 1.0 perspective division won't change the coordinates.
To create an orthographic projection matrix we make use of GLM's built-in function
glm::ortho (0.0f, 800.0f, 0.0f, 600.0f, 0.1f, 100.0f);
The first two parameters specify the left and right coordinate of the frustum and the third and fourth parameter specify the bottom and top part of the frustum. With those 4 points we've defined the size of the near and far planes and the 5th and 6th parameter then define the distances between the near and far plane. This specific projection matrix transforms all coordinates between these x, y and z range values to normalized device coordinates.
An orthographic projection matrix directly maps coordinates to the 2D plane that is your screen, but in reality a direct projection produces unrealistic results since the projection doesn't take
Perspective projection
If you ever were to enjoy the graphics the real life has to offer you'll notice that objects that are farther away appear much smaller. This weird effect is something we call

As you can see, due to perspective the lines seem to coincide at a far enough distance. This is exactly the effect perspective projection tries to mimic and it does so using a w value of each vertex coordinate in such a way that the further away a vertex coordinate is from the viewer, the higher this w component becomes. Once the coordinates are transformed to clip space they are in the range -w to w (anything outside this range is clipped). OpenGL requires that the visible coordinates fall between the range -1.0 and 1.0 as the final vertex shader output, thus once the coordinates are in clip space, perspective division is applied to the clip space coordinates:
\[ out = \begin{pmatrix} x /w \\ y / w \\ z / w \end{pmatrix} \]
Each component of the vertex coordinate is divided by its w component giving smaller vertex coordinates the further away a vertex is from the viewer. This is another reason why the w component is important, since it helps us with perspective projection. The resulting coordinates are then in normalized device space. If you're interested to figure out how the orthographic and perspective projection matrices are actually calculated (and aren't too scared of the mathematics) I can recommend this excellent article by Songho.
A perspective projection matrix can be created in GLM as follows:
glm::mat4 proj = glm::perspective (glm::radians (45.0f), (float)width/(float)height, 0.1f, 100.0f);
What
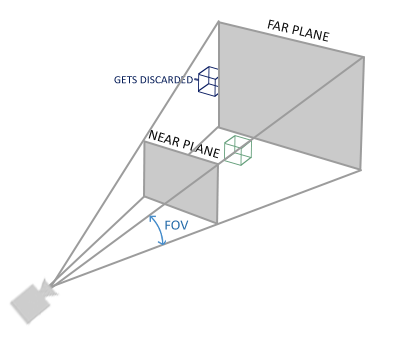
Its first parameter defines the 0.1 and the far distance to 100.0. All the vertices between the near and far plane and inside the frustum will be rendered.
10.0), OpenGL will clip all coordinates close to the camera (between 0.0 and 10.0), which can give a visual result you maybe have seen before in videogames where you could see through certain objects when moving uncomfortably close to them.
When using orthographic projection, each of the vertex coordinates are directly mapped to clip space without any fancy perspective division (it still does perspective division, but the w component is not manipulated (it stays 1) and thus has no effect). Because the orthographic projection doesn't use perspective projection, objects farther away do not seem smaller, which produces a weird visual output. For this reason the orthographic projection is mainly used for 2D renderings and for some architectural or engineering applications where we'd rather not have vertices distorted by perspective. Applications like Blender that are used for 3D modeling sometimes use orthographic projection for modeling, because it more accurately depicts each object's dimensions. Below you'll see a comparison of both projection methods in Blender:
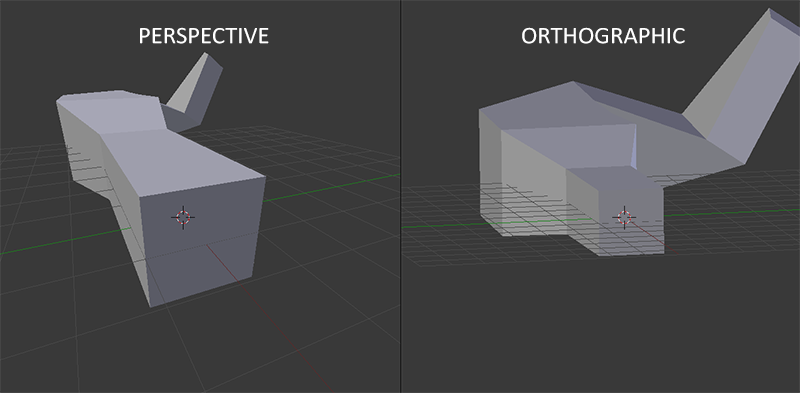
You can see that with perspective projection, the vertices farther away appear much smaller, while in orthographic projection each vertex has the same distance to the user.
Putting it all together
We create a transformation matrix for each of the aforementioned steps: model, view and projection matrix. A vertex coordinate is then transformed to clip coordinates as follows: \[ V_{clip} = M_{projection} \cdot M_{view} \cdot M_{model} \cdot V_{local} \] Note that the order of matrix multiplication is reversed (remember that we need to read matrix multiplication from right to left). The resulting vertex should then be assigned to gl_Position in the vertex shader and OpenGL will then automatically perform perspective division and clipping.
The output of the vertex shader requires the coordinates to be in clip-space which is what we just did with the transformation matrices. OpenGL then performs perspective division on the clip-space coordinates to transform them to normalized-device coordinates. OpenGL then uses the parameters from
This is a difficult topic to understand so if you're still not exactly sure about what each space is used for you don't have to worry. Below you'll see how we can actually put these coordinate spaces to good use and enough examples will follow in the upcoming chapters.
Going 3D
Now that we know how to transform 3D coordinates to 2D coordinates we can start rendering real 3D objects instead of the lame 2D plane we've been showing so far.
To start drawing in 3D we'll first create a model matrix. The model matrix consists of translations, scaling and/or rotations we'd like to apply to transform all object's vertices to the global world space. Let's transform our plane a bit by rotating it on the x-axis so it looks like it's laying on the floor. The model matrix then looks like this:
glm::mat4 model = glm::mat4(1.0f);
model = glm::rotate (model, glm::radians (-55.0f), glm::vec3(1.0f, 0.0f, 0.0f));
By multiplying the vertex coordinates with this model matrix we're transforming the vertex coordinates to world coordinates. Our plane that is slightly on the floor thus represents the plane in the global world.
Next we need to create a view matrix. We want to move slightly backwards in the scene so the object becomes visible (when in world space we're located at the origin (0,0,0)). To move around the scene, think about the following:
- To move a camera backwards, is the same as moving the entire scene forward.
Because we want to move backwards and since OpenGL is a right-handed system we have to move in the positive z-axis. We do this by translating the scene towards the negative z-axis. This gives the impression that we are moving backwards.
By convention, OpenGL is a right-handed system. What this basically says is that the positive x-axis is to your right, the positive y-axis is up and the positive z-axis is backwards. Think of your screen being the center of the 3 axes and the positive z-axis going through your screen towards you. The axes are drawn as follows:
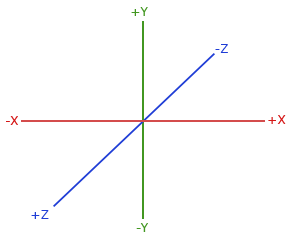
To understand why it's called right-handed do the following:
- Stretch your right-arm along the positive y-axis with your hand up top.
- Let your thumb point to the right.
- Let your pointing finger point up.
- Now bend your middle finger downwards 90 degrees.
We'll discuss how to move around the scene in more detail in the next chapter. For now the view matrix looks like this:
glm::mat4 view = glm::mat4(1.0f);
// note that we're translating the scene in the reverse direction of where we want to move
view = glm::translate (view, glm::vec3(0.0f, 0.0f, -3.0f));
The last thing we need to define is the projection matrix. We want to use perspective projection for our scene so we'll declare the projection matrix like this:
glm::mat4 projection;
projection = glm::perspective (glm::radians (45.0f), 800.0f / 600.0f, 0.1f, 100.0f);
Now that we created the transformation matrices we should pass them to our shaders. First let's declare the transformation matrices as uniforms in the vertex shader and multiply them with the vertex coordinates:
#version 330 core
layout (location = 0) in vec3 aPos;
...
uniform mat4 model;
uniform mat4 view;
uniform mat4 projection;
void main()
{
// note that we read the multiplication from right to left
gl_Position = projection * view * model * vec4(aPos, 1.0);
...
}
We should also send the matrices to the shader (this is usually done each frame since transformation matrices tend to change a lot):
int modelLoc = glGetUniformLocation (ourShader.ID, "model");
glUniform Matrix4fv(modelLoc, 1, GL_FALSE, glm::value_ptr(model));
... // same for View Matrix and Projection Matrix
Now that our vertex coordinates are transformed via the model, view and projection matrix the final object should be:
- Tilted backwards to the floor.
- A bit farther away from us.
- Be displayed with perspective (it should get smaller, the further its vertices are).
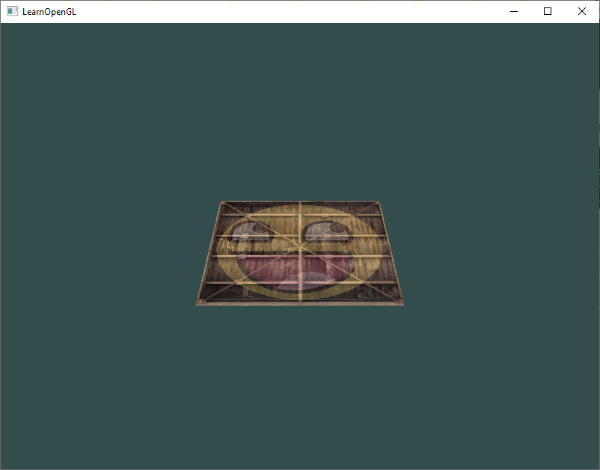
It does indeed look like the plane is a 3D plane that's resting at some imaginary floor. If you're not getting the same result, compare your code with the complete source code.
More 3D
So far we've been working with a 2D plane, even in 3D space, so let's take the adventurous route and extend our 2D plane to a 3D cube. To render a cube we need a total of 36 vertices (6 faces * 2 triangles * 3 vertices each). 36 vertices are a lot to sum up so you can retrieve them from here.
For fun, we'll let the cube rotate over time:
model = glm::rotate (model, (float)glfwGetTime () * glm::radians (50.0f), glm::vec3(0.5f, 1.0f, 0.0f));
And then we'll draw the cube using
glDrawArrays (GL_TRIANGLES, 0, 36);
You should get something similar to the following:
It does resemble a cube slightly but something's off. Some sides of the cubes are being drawn over other sides of the cube. This happens because when OpenGL draws your cube triangle-by-triangle, fragment by fragment, it will overwrite any pixel color that may have already been drawn there before. Since OpenGL gives no guarantee on the order of triangles rendered (within the same draw call), some triangles are drawn on top of each other even though one should clearly be in front of the other.
Luckily, OpenGL stores depth information in a buffer called the
Z-buffer
OpenGL stores all its depth information in a z-buffer, also known as a z value) and whenever the fragment wants to output its color, OpenGL compares its depth values with the z-buffer. If the current fragment is behind the other fragment it is discarded, otherwise overwritten. This process is called
However, if we want to make sure OpenGL actually performs the depth testing we first need to tell OpenGL we want to enable depth testing; it is disabled by default. We can enable depth testing using
glEnable (GL_DEPTH_TEST);
Since we're using a depth buffer we also want to clear the depth buffer before each render iteration (otherwise the depth information of the previous frame stays in the buffer). Just like clearing the color buffer, we can clear the depth buffer by specifying the DEPTH_BUFFER_BIT bit in the
glClear (GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
Let's re-run our program and see if OpenGL now performs depth testing:
There we go! A fully textured cube with proper depth testing that rotates over time. Check the source code here.
More cubes!
Say we wanted to display 10 of our cubes on screen. Each cube will look the same but will only differ in where it's located in the world with each a different rotation. The graphical layout of the cube is already defined so we don't have to change our buffers or attribute arrays when rendering more objects. The only thing we have to change for each object is its model matrix where we transform the cubes into the world.
First, let's define a translation vector for each cube that specifies its position in world space. We'll define 10 cube positions in a glm::vec3 array:
glm::vec3 cubePositions[] = {
glm::vec3( 0.0f, 0.0f, 0.0f),
glm::vec3( 2.0f, 5.0f, -15.0f),
glm::vec3(-1.5f, -2.2f, -2.5f),
glm::vec3(-3.8f, -2.0f, -12.3f),
glm::vec3( 2.4f, -0.4f, -3.5f),
glm::vec3(-1.7f, 3.0f, -7.5f),
glm::vec3( 1.3f, -2.0f, -2.5f),
glm::vec3( 1.5f, 2.0f, -2.5f),
glm::vec3( 1.5f, 0.2f, -1.5f),
glm::vec3(-1.3f, 1.0f, -1.5f)
};
Now, within the render loop we want to call
glBindVertexArray (VAO);
for(unsigned int i = 0; i < 10; i++)
{
glm::mat4 model = glm::mat4(1.0f);
model = glm::translate (model, cubePositions[i]);
float angle = 20.0f * i;
model = glm::rotate (model, glm::radians (angle), glm::vec3(1.0f, 0.3f, 0.5f));
ourShader.setMat4("model", model);
glDrawArrays (GL_TRIANGLES, 0, 36);
}
This snippet of code will update the model matrix each time a new cube is drawn and do this 10 times in total. Right now we should be looking into a world filled with 10 oddly rotated cubes:
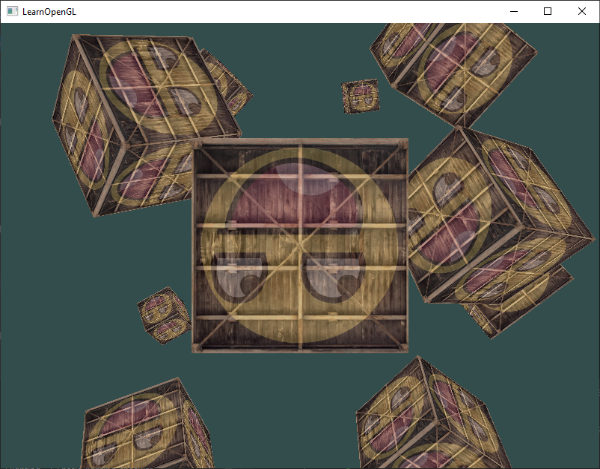
Perfect! It looks like our container found some like-minded friends. If you're stuck see if you can compare your code with the source code.
Exercises
- Try experimenting with the
FoVandaspect-ratioparameters of GLM'sprojectionfunction. See if you can figure out how those affect the perspective frustum. - Play with the view matrix by translating in several directions and see how the scene changes. Think of the view matrix as a camera object.
- Try to make every 3rd container (including the 1st) rotate over time, while leaving the other containers static using just the model matrix: solution.




